apriori && fpgrowth:频繁模式与关联规则挖掘

发表于 | 分类于 | 0 comments
阅读次数:   |   字数统计: 4.4k(字)   |   阅读时长: 20(分)

详细代码实现放在我的github上:click me

一、实验说明

1.1 任务描述

1.2 数据集说明

  • GroceryStore数据集

    This data set contains transaction records of a grocery store in a month. Each line is a transaction, where the purchased items line in {}, separated by “,” (the space is replaced by “/”). In total, there are 9835 transactions of 169 items.

  • UNIX_usage数据集

    The data set contains 9 sets of sanitized user data drawn from the
    command histories of 8 UNIX computer users at Purdue over the course
    of up to 2 years (USER0 and USER1 were generated by the same person,
    working on different platforms and different projects). The data is
    drawn from tcsh(1) history files and has been parsed and sanitized to
    remove filenames, user names, directory structures, web addresses,
    host names, and other possibly identifying items. Command names,
    flags, and shell metacharacters have been preserved. Additionally,
    SOF and EOF tokens have been inserted at the start and end of
    shell sessions, respectively. Sessions are concatenated by date order
    and tokens appear in the order issued within the shell session, but no
    timestamps are included in this data.

    For example, the two sessions:

    # Start session 1
cd ~/private/docs
ls -laF | more
cat foo.txt bar.txt zorch.txt > somewhere
exit
# End session 1

# Start session 2
cd ~/games/
xquake &
fg
vi scores.txt
mailx john_doe@somewhere.com
exit
# End session 2

    would be represented by the token stream
    ​
    ​ SOF
    ​ cd
    ​ <1> # one “file name” argument
    ​ ls
    ​ -laF
    ​ |
    ​ more
    ​ cat
    ​ <3> # three “file” arguments
    ​ >
    ​ <1>
    ​ exit
    ​ EOF
    ​ SOF
    ​ cd
    ​ <1>
    ​ xquake
    ​ &
    ​ fg
    ​ vi
    ​ <1>
    ​ mailx
    ​ <1>
    ​ exit
    ​ EOF

二、代码设计与实现

对apriori算法手动实现了一个dummy版本和一个advanced版本，dummy版本没有使用剪枝的trick，使用暴力的方法生成候选项级，対事务表不做任何处理。而advanced版本则在dummy版本的基础上加入了一剪枝的trick，性能更胜一筹。对fpgrowth算法使用了已有的python包，其中的实现细节没有深入去review了。下面对这几份代码的详细设计与实现做一个说明。

2.1 dummy apriori

从命令行接收算法的控制参数

1
2
3
4
5
6
if len(sys.argv) != 4:
	print('usage: python apriori_dummy.py dataset-path support-ratio K')
else:
	dataset_path_name = sys.argv[1] # 要处理的数据集GroceryStore or UNIX_usage
	min_sup = float(sys.argv[2])  # 支持率
	itemset_size = int(sys.argv[3])  # 要挖掘的最大频繁项集大小

读取数据集之后每一事务以set形式存储在一个列表data中，然后匹配、统计生成频繁一项集：

1
2
3
4
5
6
7
8
9
10
11
oneitem_freq = {}
for itemset in data:
    for item in itemset:
        oneitem_freq[item] = 0
for itemset in data:
    for item in itemset:
        oneitem_freq[item] += 1
oneitem_freqset = []
for oneitem in oneitem_freq.keys():
    if oneitem_freq[oneitem] >= frequency_threshold:
        oneitem_freqset.append([oneitem])

接下来就进入循环过程：由k项频繁项集生成k+1项候选项集，然后匹配事务表统计频次，筛选出高于支持率对应频次的作为k+1项频繁项集，以此往复循环直到生成的频繁项集为空或者达到要挖掘的频繁项集大小的上限。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
pre_freqset = oneitem_freqset
for k in range(2, itemset_size + 1):
    start_time = time.time()
    candidates_k = generate_candidates(pre_freqset)
    k_item_freq = count_freqset(data, candidates_k)
    pre_freqset = []
    new_k_item_freq = {}
    for key in k_item_freq.keys():
        if k_item_freq[key] >= frequency_threshold:
            pre_freqset.append(sorted(key.split(',')))
            new_k_item_freq[','.join(pre_freqset[-1])] = k_item_freq[key]
    k_item_freq = new_k_item_freq
    if len(pre_freqset) == 0:
        break
    pre_freqset.sort()
    output(pre_freqset, k_item_freq, frequency_threshold, k, dataset_path_name)

这段主控制程序中调用了2个甚为关键的函数：generate_candidates用于生成候选项集，count_freqset用于匹配事务表进行统计。

generate_candidates: 使用纯暴力拼接的方式，由上一轮的k频繁项集构成的单项元素集合中每一个元素与任一k频繁项连接(前提是该单项元素不出现在这一频繁项中)构成一个k+1候选项

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
def generate_candidates(pre_freqset):
    """
    由k-1的频繁项集生成k候选项集
    :param pre_freqset: 前一次生成的k-1频繁项集
    :param k: 要生成的k频繁项集对应的k
    :return: 包含k候选项集的列表
    """
    items = []
    for itemset in pre_freqset:
        for item in itemset:
            items.append(item)
    items = list(set(items))
    candidates = []
    for itemset in pre_freqset:
        for item in items:
            if item not in itemset:
                itemset_backup = copy.deepcopy(itemset)
                itemset_backup.append(item)
                candidates.append(','.join(sorted(itemset_backup)))
    candidates_unique = []
    candidates = set(candidates)
    for can in candidates:
        candidates_unique.append(can.split(','))
    return candidates_unique

count_freqset: 对由generate_candidates生成的每一候选项在事务表中扫描匹配，统计出现频次

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def count_freqset(data, candidates_k):
    """
    对照事务表统计候选项集频次
    :param data: 事务集
    :param candidates_k: k候选项集
    :return: 候选项映射到频次的dict
    """
    counter = {}
    for can in candidates_k:
        canset = set(can)
        canstr = ','.join(can)
        counter[canstr] = 0
        for itemset in data:
            if canset <= itemset:
                counter[canstr] += 1
    return counter

2.2 advanced apriori

advanced apriori在dummy apriori的基础上加入了一些剪枝的技巧，包括减小生成候选项集的规模、不断减少事务表规模、减少事务表中元组中的项。

  • 减小生成候选项集规模

    如果一个k+1候选项是频繁的，那么生成它的k频繁项集中必包含其k+1个子集。例如，如果{t1, t2, t3, t5}是频繁的，那么它将由{t1, t2, t3}和{t1, t2,t5 }生成，否则它就不会被生成。这么做要求生成候选项集的频繁项集的项内是有序的，各项之间也是有序的。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    def generate_candidates(pre_freqset, k):
        """
        由k-1的频繁项集生成k候选项集
        :param pre_freqset: 前一次生成的k-1频繁项集（项内与项之间都为有序状态）
        :param k: 要生成的k频繁项集对应的k
        :return: 包含k候选项集的列表
        """
        candidates = []
        if k == 2:
            for i in range(len(pre_freqset)):
                for j in range(i + 1, len(pre_freqset)):
                    candidates.append([pre_freqset[i][0], pre_freqset[j][0]])
        else:
            i = 0
            while i < len(pre_freqset) - 1:
                tails = []
                while i < len(pre_freqset) - 1 and pre_freqset[i][:-1] == pre_freqset[i + 1][:-1]:
                    tails.append(pre_freqset[i][-1])
                    i += 1
                if tails:
                    tails.append(pre_freqset[i][-1])
                    prefix = copy.deepcopy(pre_freqset[i][0:-1])
                    for a in range(len(tails)):
                        for b in range(a + 1, len(tails)):
                            items = copy.deepcopy(prefix)
                            items.append(tails[a])
                            items.append(tails[b])
                            candidates.append(items)
                i += 1

        return candidates

  • 减小事务表规模

    如果一个k+1项候选项能与事务表中一条记录匹配，那么其k+1个子集也必能与事务表中该条记录匹配。因此在事务表中匹配k候选项集的时候，统计每条记录被匹配到的次数，如果少于k+1次，那么将该条记录从事务表中移除，因为它绝不可能与下一轮的任一k+1项候选项匹配。这样每次迭代都减小了事务表的规模，从而减小扫描事务表的时间消耗

  • 减少事务表中元组的项

    如果事务表中元组的某一项能包含在一个k+1频繁项中，那么该项比出现在这个k+1频繁项的k个k项子集中。所以在扫描事务表统计k项候选集的出现频次时，如果事务表中任一元组的某一项未被匹配中k次,那么该项将在筛选出k频繁项集后从元组中除去，从而减少统计k+1项候选集频次时与事务表中元组的匹配次数。具体实现在减少事务表规模实现的基础上稍作修改即可，下面是结合减少事务表规模以及表中元组项数的实现

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    def count_freqset(data, candidates_k):
        """
        对照事务表统计候选项集频次
        :param data: 事务集
        :param candidates_k: k候选项集
        :return: 候选项映射到频次的dict
        """
        prune_basis = []
        for itemset in data:
            prune_basis.append([0] * (len(itemset) + 1))
        counter = {}
        for can in candidates_k:
            canset = set(can)
            canstr = ','.join(can)
            counter[canstr] = 0
            for i in range(len(data)):
                if canset <= data[i]:
                    counter[canstr] += 1
                    prune_basis[i][-1] += 1
                    j = 0
                    for item in data[i]:
                        if item in canset:
                            prune_basis[i][j] += 1
                        j += 1
        return counter, prune_basis

    def prune(data, prune_basis, k):
        """
        由k-1的频繁项集生成k候选项集
        :param data: 存储事务的列表
        :param prune_basis: 由k候选项集匹配事务表时生成的剪枝依据
        :param k: 为生成k+1频繁项集剪枝
        :return: None
        """
        # 删除列表中某一项之后列表元素会自动往前补位,即被删除元素后的元素对应索引-1
        if len(prune_basis) != 0:
            h = 0
            for i in range(len(prune_basis)):
                if prune_basis[i][-1] < k + 1:
                    del data[h]
                else:
                    j = 0
                    del_items = []
                    for item in data[h]:
                        if prune_basis[i][j] < k:
                            del_items.append(item)
                        j += 1
                    for item in del_items:
                        data[h].remove(item)
                    h += 1

2.3 基于apriori的频繁项集挖掘关联规则

基于每论迭代得到的k-频繁项集，对其中每一k-频繁项利用二进制法构造其所有势大于0的子集

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def get_all_subsets(itemset):
    """
    计算itemset的所有势大于0的子集
    :param itemset: 包含一个项集的列表 
    :return: 项集itemset的所有势大于0的子集(type: list(set...))
    """
    n = len(itemset)
    all_subsets = []
    for i in range(1, 2**(n - 1)):
        subset = set()
        for j in range(n):
            if (i >> j) % 2 == 1:
                subset.add(itemset[j])
        all_subsets.append(subset)
    return all_subsets

任一子集与该子集和生成它的父集k-频繁项之间的差集构造k项的关联规则，筛选出大于置信度且提升度大于1.0的关联规则作为要挖掘的强关联规则

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def generate_association_rules(k_freqset, itemset_freq, min_con, dataset_size):
    """
    生成关联规则
    :param k_freqset: k频繁项集 
    :param itemset_freq: 项集与频次之间的字典映射
    :param min_con: 置信度
    :param dataset_size: 数据集记录总数
    :return: 关联规则列表(list(list(previous item, post item, frequency)...))
    """
    association_rules = []
    for i in range(len(k_freqset)):
        all_subsets = get_all_subsets(k_freqset[i])
        par_set = set(k_freqset[i])
        par_cnt = itemset_freq[','.join(k_freqset[i])]
        for subset in all_subsets:
            subset_str = ','.join(sorted(list(subset)))
            diffset_str = ','.join(sorted(list(par_set.difference(subset))))
            subset_cnt = itemset_freq[subset_str]
            diffset_cnt = itemset_freq[diffset_str]
            subset_prob = 1.0 * subset_cnt / dataset_size
            diffset_prob = 1.0 * diffset_cnt / dataset_size
            if 1.0 * par_cnt / subset_cnt >= min_con and 1.0 * par_cnt / (subset_cnt * diffset_prob) >= 1.0:
                association_rules.append([subset_str, diffset_str, 1.0 * par_cnt / subset_cnt])
            elif 1.0 * par_cnt / diffset_cnt >= min_con and 1.0 * par_cnt / (diffset_cnt * subset_prob) >= 1.0:
                association_rules.append([diffset_str, subset_str, 1.0 * par_cnt / diffset_cnt])

    return association_rules

2.4 fpgrowth

这里没有多少要讲的，直接调用接口

1
2
3
4
5
6
7
import pyfpgrowth

data = []
read(data, dataset_path_name)

freq_patterns = pyfpgrowth.find_frequent_patterns(data, frequency_threshold)
association_rules = pyfpgrowth.generate_association_rules(freq_patterns, min_con)

三、实验结果及分析对比

3.1 实验结果展示

  • apriori算法在UNIX_usage数据集上挖掘的频繁5-项集的一部分(支持度0.01)
1
2
3
4
5
6
7
8
9
10
11
12
13
&,-l,<1>,<2>,cd : 131
&,<1>,<2>,>,cd : 142
&,<1>,<2>,>,rm : 111
&,<1>,<2>,cd,cp : 139
&,<1>,<2>,cd,ll : 193
&,<1>,<2>,cd,ls : 198
&,<1>,<2>,cd,mv : 155
&,<1>,<2>,cd,rm : 217
&,<1>,<2>,cd,vi : 209
&,<1>,<2>,ll,rm : 127
&,<1>,<2>,ll,vi : 132
&,<1>,<2>,ls,rm : 127
&,<1>,<2>,mv,rm : 114
  • apriori算法在GroceryStore数据集上挖掘的频繁3-项集的一部分(支持度0.01)
1
2
3
4
5
6
7
8
9
10
bottled water,other vegetables,whole milk : 106
butter,other vegetables,whole milk : 113
citrus fruit,other vegetables,root vegetables : 102
citrus fruit,other vegetables,whole milk : 128
citrus fruit,whole milk,yogurt : 101
curd,whole milk,yogurt : 99
domestic eggs,other vegetables,whole milk : 121
fruit/vegetable juice,other vegetables,whole milk : 103
other vegetables,pastry,whole milk : 104
other vegetables,pip fruit,whole milk : 133
  • apriori算法在GroceryStore数据集上挖掘的一些关联规则(支持度0.01，置信度：0.5)
1
2
3
4
5
6
7
butter,other vegetables -> whole milk	confidence:0.5736040609137056
citrus fruit,root vegetables -> other vegetables	confidence:0.5862068965517241
curd,yogurt -> whole milk	confidence:0.5823529411764706
domestic eggs,other vegetables -> whole milk	confidence:0.5525114155251142
other vegetables,pip fruit -> whole milk	confidence:0.5175097276264592
rolls/buns,root vegetables -> other vegetables	confidence:0.502092050209205
root vegetables,tropical fruit -> other vegetables	confidence:0.5845410628019324
  • fpgrowth算法在GroceryStore数据集上挖掘的一些关联规则(置信度0.5)
1
2
3
4
5
curd,yogurt -> whole milk	confidence: 0.5823529411764706
butter,other vegetables -> whole milk	confidence: 0.5736040609137056
domestic eggs,other vegetables -> whole milk	confidence: 0.5525114155251142
other vegetables,whipped/sour cream -> whole milk	confidence: 0.5070422535211268
other vegetables,pip fruit -> whole milk	confidence: 0.5175097276264592

  • apriori算法在UNIX_usage数据集上挖掘的一些关联规则a -> b(支持度0.01， 置信度：0.8)

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    & -> <1>	confidence:0.8453738910012675
    netscape -> &	confidence:0.8895705521472392
    &,-l -> <1>	confidence:0.9875776397515528
    &,-l -> <2>	confidence:0.8509316770186336
    &,-l -> <1>,<2>	confidence:0.84472049689441
    &,-l,<2> -> <1>	confidence:0.9927007299270073
    &,>,rm -> <1>,<2>	confidence:0.9024390243902439
    &,<2>,cd,cp -> <1>	confidence:1.0
    -,<1>,k,ll -> <2>,cd	confidence:0.959349593495935
    -,k,ll -> <1>,<2>,cd	confidence:0.959349593495935
    <1>,<2>,cp,ls,mv,rm -> cd	confidence:0.9888888888888889
    <2>,cp,ls,mv,rm -> <1>,cd	confidence:0.9888888888888889
    <n2>,cd,cp,ls,mv,rm,vi -> <1>	confidence:1.0
    <1>,cd,cp,ls,mv,rm,vi -> <2>	confidence:1.0

从上面挖掘出的关联规则可以发现，GroceryStore数据集的相关度很低，将置信度调到0.5的才挖掘到少量的关联规则，但是置信度不高并不一定代表它就没什么意义，上面列出的几条规则人眼观察还是很合理的，从如此多的数据记录中只挖掘出少量的几条关联规则使其更直观更具有参考价值，挖出太多关联规则反而更容易让人眼花缭乱，从而失去判断。反观在UNIX_usage上挖掘出的关联规则，置信度高而且数量又多，但很多都看起来让人难以理解，意义不大，但还是可以大致看出来哪些命令经常一起共用。fpgrowth算法在UNIX_usage数据集上运行时递归深度太深而没能跑出结果来。

3.2 时间性能对比

3.2.1 频繁项集挖掘

3.2.1.1 UNIX_usage Dataset

对比dummy apriori，仅剪枝候选项集规模的advanced_1 apriori，剪枝候选项集规模和事务表规模的advanced_2 apriori，剪枝候选项集规模和事务表规模以及表中元组项数的advanced_3 apriori在相同数据集、实验环境和实验参数下的时间损耗(单位：秒/s)

实验参数与数据集：

支持度：0.01

最大频繁项大小：10

数据集：UNIX_usage

下面表格中以da表示dummy apriori，a1a表示advance_1 apriori,a2a表示advanced_2 apriori,a3a表示advanced_3 apriori

表 1 apriori在UNIX_usage数据集上的频繁项集挖掘时耗(秒/s)
freq-1 freq-2 freq-3 freq-4 freq-5 freq-6 freq-7 freq-8
da 0.021 2.156 17.066 33.359 35.156 17.190 2.522 0.183
a1a 0.016 2.960 5.234 5.808 2.812 0.675 0.128 0.007
a2a 0.019 2.962 3.208 2.758 1.200 0.246 0.027 0.001
a3a 0.017 3.311 3.997 3.658 1.663 0.413 0.051 0.002
3.2.1.2 GroceryStore Dataset

实验参数与数据集：

支持度：0.01

最大频繁项大小：10

数据集：GroceryStore

表 2 apriori在GroceryStore数据集上的频繁项集挖掘时耗(秒/s)
freq-1 freq-2 freq-3
da 0.019 1.255 2.547
a1a 0.014 1.978 0.402
a2a 0.012 1.982 0.263
a3a 0.014 2.254 0.322

3.2.2 关联规则挖掘

由于关联规则挖掘依赖频繁项集挖掘,选择上述时间性能最好的apriori算法来实现关联呢规则挖掘

3.2.2.1 UNIX_usage Dataset

实验参数与数据集：

支持度：0.01

最大频繁项大小：10

置信度：0.8

数据集：UNIX_usage

表 3 UNIX_usage数据集上的关联规则挖掘时耗(秒/s)
2-items 3-items 4-items 5-items 6-items 7-items 8-items
apiori 2.840 3.092 2.619 1.779 0.268 0.035 0.003
3.2.2.2 GroceryStore Dataset

实验参数与数据集：

支持度：0.01

最大频繁项大小：10

置信度：0.5

数据集：GroceryStore

表 4 GroceryStore数据集上的关联规则挖掘时耗(秒/s)
3-items
apriori 0.286

3.2.3 简要分析

从两个数据集的表现来看，advanced_2 apriori性能是最好的，advanced_1 apriori性能与advanced_2 apriori性能相近，在较小的数据集GroceryStore上差距在毫秒级别，在较大数据集UNIX_usage上差距在几秒以内。advanced_3 apriori理想情况下应该是性能最好的，因其使用了最多的剪枝技巧，但是实际情况却并非如此，用在删减事务表中元组项的时间比其能优化的时间还要多，得不偿失，如果能删除较多的元组项就能带来不错的性能提升，所以这一剪枝的trick能否有效还是要视数据集而定，不同的数据集上优化效果也不一样。而advanced apriori的三个算法相比dummy apriori在时间性能上提升了好几倍。由此可知，时间性能的主要提升点在减小候选项集规模，减小事务表规模的时间性能提升效果不明显，但是当数据规模较大时也能带来秒级的性能提升。在aporiori挖掘出的频繁项集基础上挖掘强关联规则的时间消耗基本与只作频繁项集挖掘的时间消一致，这是因为k-频繁项的k还比较小，生成的子集不多，相对于候选集生成与数据记录扫描匹配的时间复杂度可忽略不计，这才使得两者时间消耗基本一致。当频繁项足够长时，子集的数目是呈指数增长的，那是复杂度将变得让人难以接受，因此使用apriori挖掘关联规则时最好限制要挖掘的最大频繁项的大小。

3.3 内存占用对比

3.3.1 UNIX_usage Dataset

实验参数与数据集：

最小支持度：0.01

最大频繁项大小：10

数据集：UNIX_usage

  • dummy apriori频繁项集挖掘

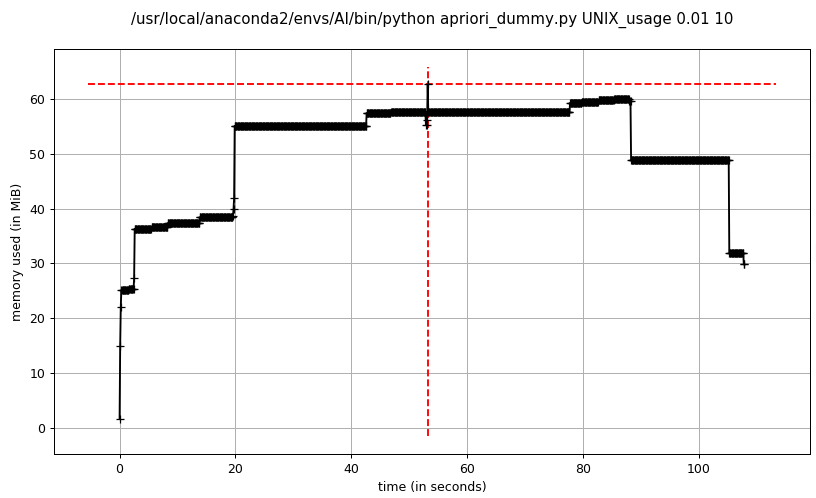
  • advanced_1 apriori频繁项集挖掘

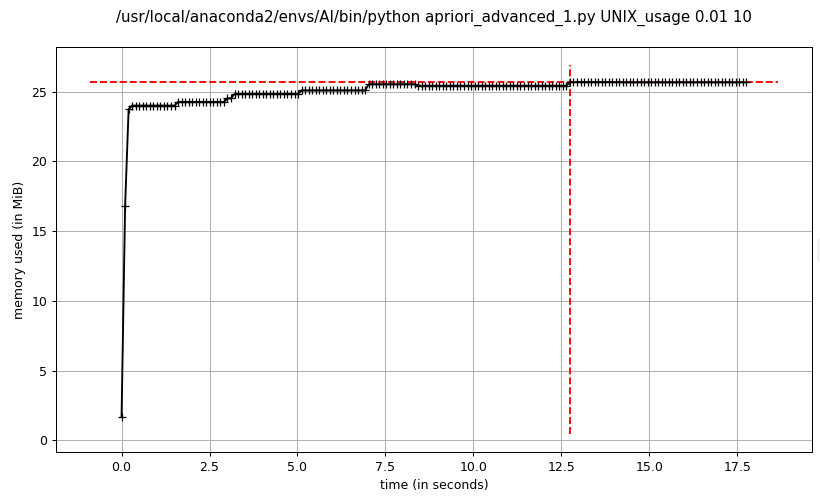
  • advanced_2 apriori频繁项集挖掘

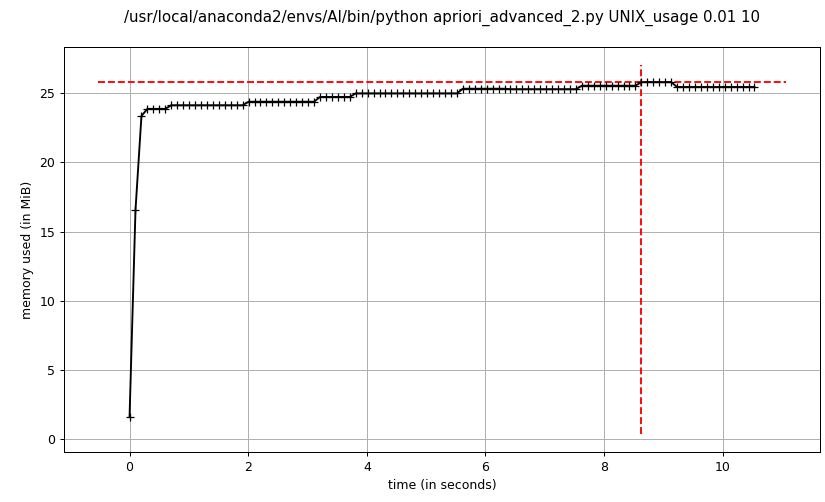
  • advanced_3 apriori频繁项集挖掘

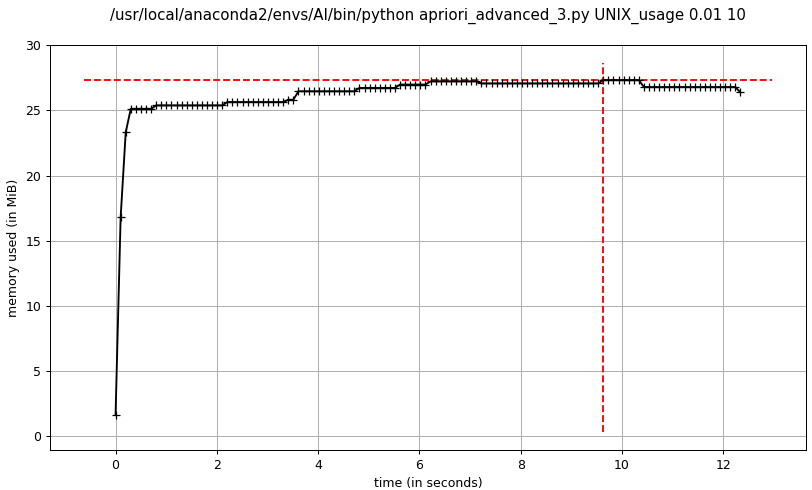
  • advanced_2 apriori关联规则挖掘

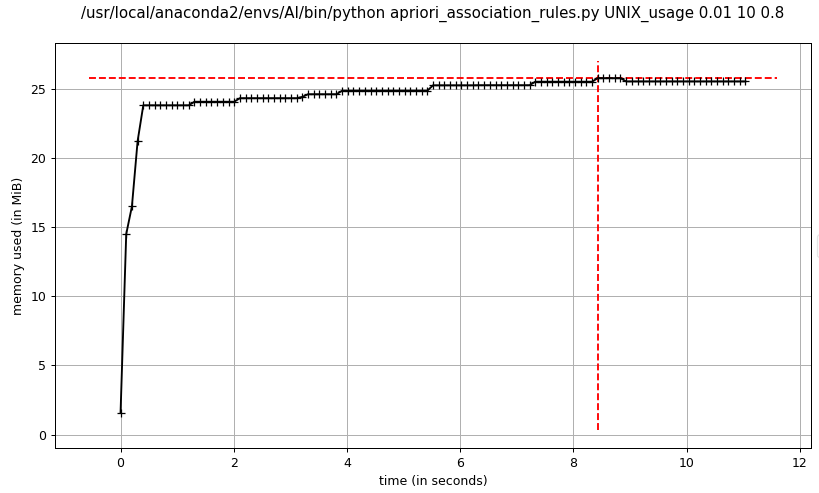
3.3.2 GroceryStore Dataset

实验参数与数据集：

支持度：0.01

最大频繁项大小：10

置信度：0.5

数据集：GroceryStore

  • dummy apriori频繁项集挖掘

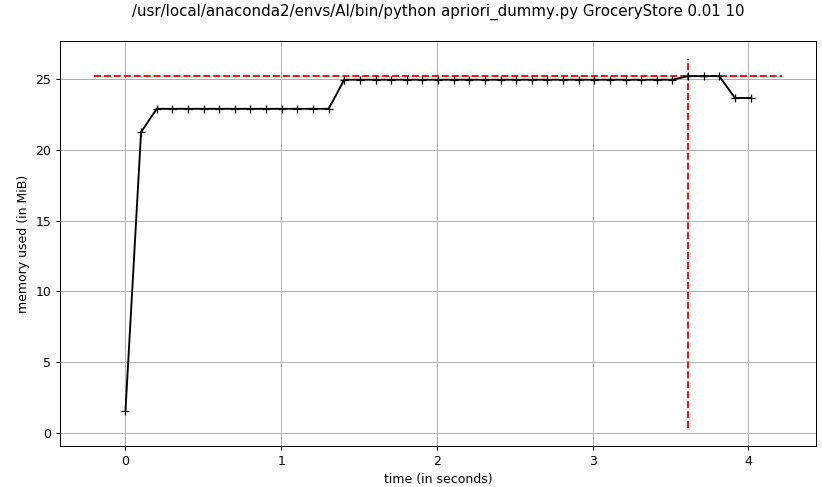
  • advanced_1 apriori频繁项集挖掘

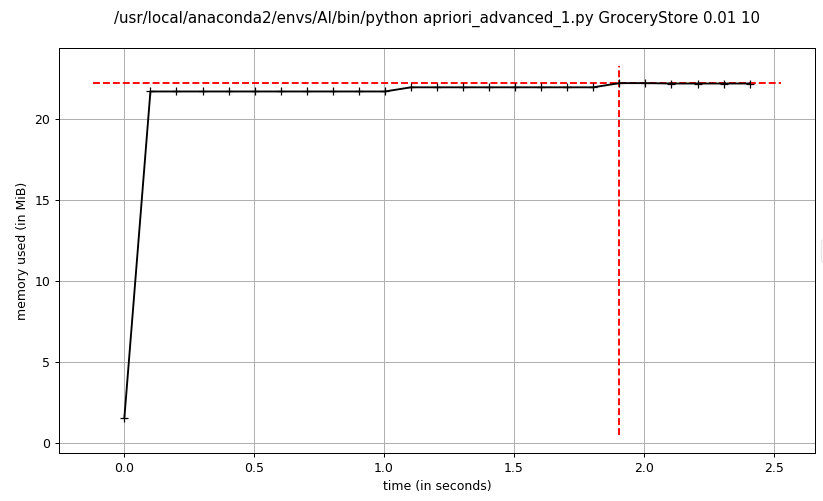
  • advanced_2 apriori频繁项集挖掘

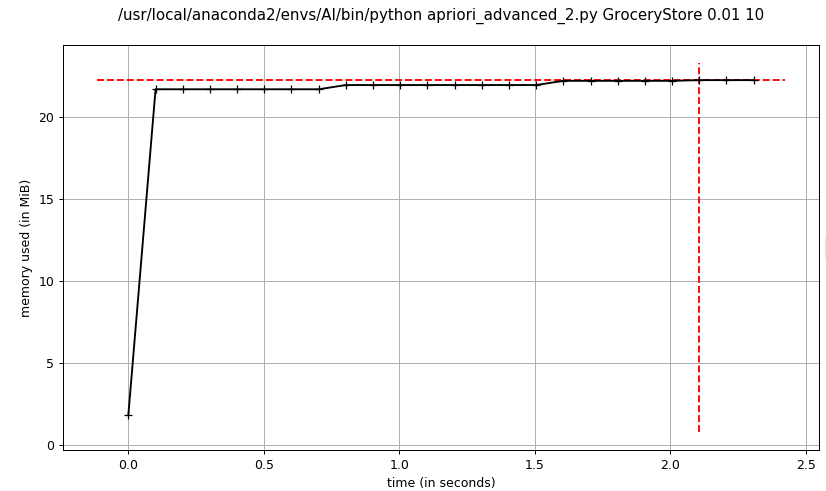
  • advanced_3 apriori频繁项集挖掘

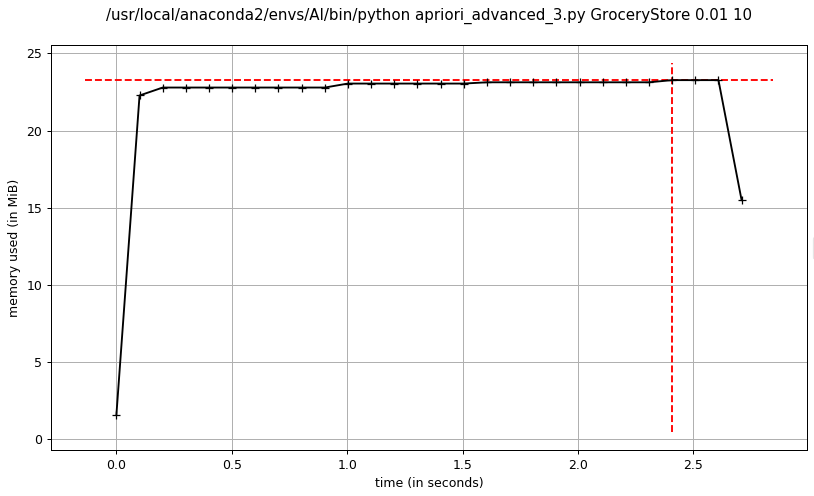
  • advanced_2 apriori关联规则挖掘

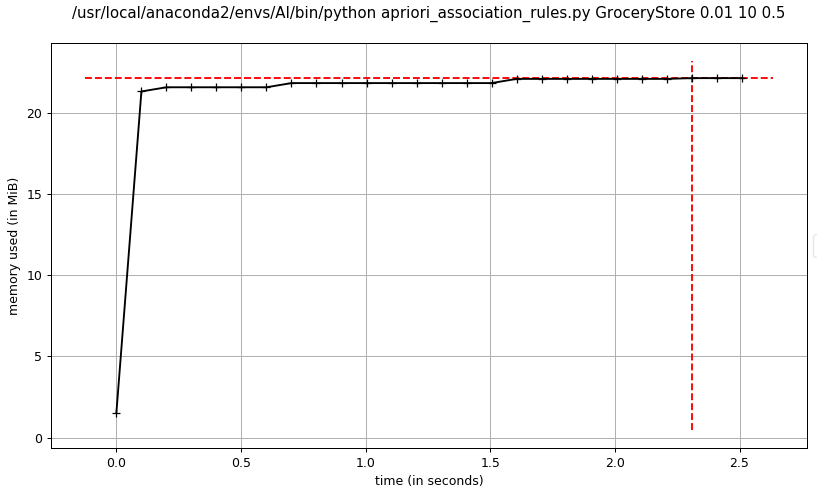
  • fpgrowth关联规则挖掘

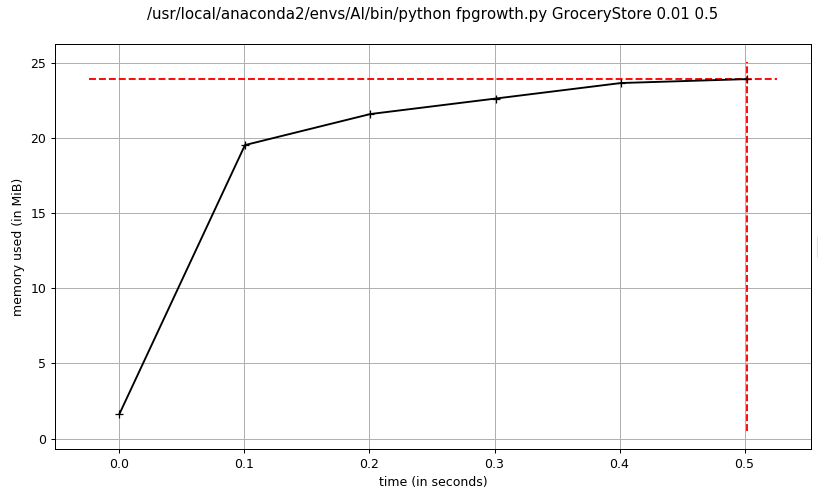
3.3.3 简要分析对比

advanced_1 apriori和advanced_2 apriori的内存消耗基本一致，在程序运行期间比较平稳，而dummy apriori相比advanced apriori占用内存较大，峰值达到了advanced apriori的2倍以上，主要消耗在暴力穷举候选项集，导致候选项集规模太大，占用内存过多。

---------------- The End ----------------

作者: brooksjay
联系邮箱: jaypark@smail.nju.edu.cn
本文地址: https://brooksj.com/2019/04/24/apriori-fpgrowth/
本文基于 知识共享署名-相同方式共享 4.0 国际许可协议发布
转载请注明出处, 谢谢！