Word2Vec原理详解

paper

简介

Word2Vec分为CBOW模型(Continuous Bag-of-Words Model)和Skip-gram(Continuous Skip-gram Model)模型,如下图所示

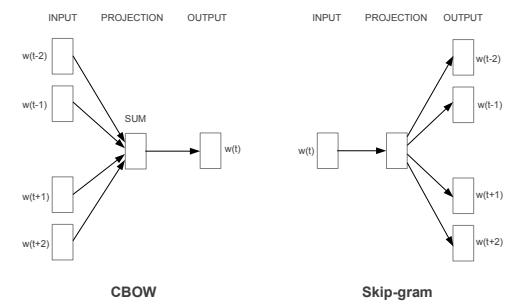
当训练文本集规模较小时适合使用CBOW模型，当训练文本集规模较大时适合使用Skip-gram模型

训练方法

Hierarchical Softmax

方法一：基于Huffman树的Hierarchical Softmax

Negative Sampling

方法二：作者Mikolov提出的Negative Sampling(NEG)，该方法是Noise Contrastive Estimation(NCE)的一个简化版本

CBOW模型

在CBOW模型中，已知词$w$的上下文$Context(w)$，需要预测$w$，因此对于给定的$Context(w)$，词$w$就是一个正样本，其它词就是负样本了。假定现在已经选好了一个关于$w$的负样本子集$NEG(w) \ne \emptyset$，且对$\forall\ \widetilde{w} \in \mathcal{D}$，定义

$L^{w}(\widetilde{w})=\begin{cases} 1,& {\widetilde{w}}=w; \\ 0,& {\widetilde{w}} \ne w; \end{cases}\tag{1.1}$

令$\sigma(x)=\frac{1}{1+\mathrm{e}^{x}}$，语料库$C$，概率生成函数如下

$\begin{align} G&=\prod_{w \in C}{g(\mathcal{w})} \\ &=\prod_{w \in C}\prod_{u \in \{w\} \cup NEG(w)}{p(u|Context(w))} \end{align}\tag{1.2}$

其中

$p(u|Context(w))=\begin{cases} \sigma({x_{w}^{T}\theta^{u})},& L^{w}(u)=1\\ 1-\sigma(x_{w}^{T}\theta^{u}), & L^{w}(u)=0 \end{cases}\tag{1.3}$

可将$p(u|Context(w))$写成整体表达式如下

$p(u|Context(w))=[\sigma({x_{w}^{T}\theta^{u}})]^{L^{w}(u)} \cdot [1-\sigma(x_{w}^{T}\theta^{u})]^{1-L^{w}(u)}\tag{1.4}$

从而$g(w)$可简写为

$g(w)=\sigma({x_{w}^{T}\theta^{w}})\prod_{u \in NEG(w)}{[1 - \sigma({x_{w}^{T}\theta^{u}})]}\tag{1.5}$

最终的目标函数对G取对数求最大似然。从形式上看，最大化$g(w)$相当于最大化 $\sigma({x_{w}^{T}\theta^{w}})$ ，同时最小化所有的 $\sigma({x_{w}^{T}\theta^{u}}),u \in NEG(w)$ ，使得增大正样本概率的同时降低负样本的概率，这正是我们所希望看到的结果

$\begin{align} \mathcal{L}&=\log{G}=\log\prod_{w \in \mathcal{C}}g(w)=\sum_{w \in \mathcal{C}}\log{g(w)} \\ &=\sum_{w \in \mathcal{C}}\sum_{u \in \{w\} \cup NEG(w)}\{L^{w}(u) \cdot \log[\sigma(x_{w}^{T}\theta^{u})]+[1-L^{w}(u)] \cdot \log[1-\sigma({x_{w}^{T}\theta^{u}})]\} \end{align}\tag{1.6}$

为方便梯度推导，将(1.6)式花括号中的内容简记为$\mathcal{L}(w,u)$，即

$\mathcal{L}(w,u)=L^{w}(u) \cdot \log[\sigma({x_{w}^{T}\theta^{u}})]+[1-L^{w}(u)] \cdot \log{[1-\sigma({x_{w}^{T}\theta^{u}})]} \tag{1.7}$

利用梯度上升法对$\mathcal{L}$进行优化求最大值，$\mathcal{L}(w,u)$分别对$x_{w}和\theta^{u}$求偏导

$\begin{align} \frac{\partial\mathcal{L}(w,u)}{\partial\theta^{u}}&=\frac{\partial}{\partial\theta^{u}}\{L^{w}(u) \cdot \log[\sigma(x_{w}^{T}\theta^{u})]+[1-L^{w}(u)] \cdot \log[1-\sigma({x_{w}^{T}\theta^{u}})]\}\\ &=L^{w}(u)[1-\sigma(x_{w}^{T}\theta^{u}]x_{w}-[1-L^{w}(u)]\sigma(x_{w}^{T}\theta^{u})x_{w}\\ &=\{L^{w}(u)[1-\sigma(x_{w}^{T}\theta^{u}]-[1-L^{w}(u)]\sigma(x_{w}^{T}\theta^{u})\}x_{w}\\ &=[L^{w}(u)-\sigma(x_{w}^{T}\theta^{u})]x_{w} \end{align}\tag{1.8}$

于是$\theta^{u}$的更新公式可写成

$\theta^{u}=\theta^{u}+\eta[L^{w}(u)-\sigma(x_{w}^{T}\theta^{u})]x_{w} \tag{1.9}$

接下来考虑$\mathcal{L}(w,u)$对 $x_{w}$ 的偏导，由于式(1.7)中 $x_{w}$ 和 $\theta^{u}$ 的对称性可得

$\frac{\partial\mathcal{L}(w,u)}{\partial{x_{w}}}=[L^{w}(u)-\sigma(x_{w}^{T}\theta^{u})]\theta^{u} \tag{1.10}$

于是，利用式(1.10)的结果可得$v(\widetilde{w}),\widetilde{w} \in Context(w)$的更新公式为

$v(\widetilde{w})=v(\widetilde{w}) + \eta\sum_{u \in \{w\} \cup NEG(w)}\frac{\partial\mathcal{L}(w,u)}{\partial{x_{w}}} \tag{1.11}$

伪代码如下

Skip-gram模型

结合SKip-gram和CBOW模型的区别，将优化目标函数由原来的$G=\prod_{w \in C}g(w)$改写为

$G=\prod_{w \in C}\prod_{u \in Context(w)}g(u) \tag{2.1}$

这里，$\prod_{u \in Context(w)}g(u)$表示对于一个给定的样本$(w,Context(w))$，我们希望最大化的量，$g(u)$类似于上一节$g(w)$，定义为

$g(u)=\prod_{z \in \{u\} \cup NEG(u)}p(z|w) \tag{2.2}$

其中$NEG(u)$表示处理词u时生成的负样本子集，条件概率

$p(z|w)=\begin{cases} \sigma(v(w)^T\theta^z),& L^{u}(z)=1\\ 1-\sigma(v(w)^T\theta^z),& L^{u}(z)=0 \end{cases}\tag{2.3}$

(2.3)式写成整体表达式为

$p(z|w)=[\sigma(v(w)^T\theta^{z}]^{L^{u}(z)} \cdot [1-\sigma(v(w)^{T}\theta^{z})]^{1-L^{u}(z)} \tag{2.4}$

同样，我们取G的对数，最终的目标函数为

$\begin{align} \mathcal{L}=\log{G}&=log\prod_{w \in C}\prod_{u \in Context(w)}\prod_{z \in \{u\} \cup NEG(u)}p(z|w)\\ &=\sum_{w \in C}\sum_{u \in Context(w)}\sum_{z \in \{u\} \cup NEG(u)}\log{p(z|w)}\\ &=\sum_{w \in C}\sum_{u \in Context(w)}\sum_{z \in \{u\} \cup NEG(u)}\{L^{u}(z) \cdot \log{[\sigma(v(w)^T\theta^{z})]} + [1-L^{u}(z)]\log{[1-\sigma(v(w)^{T}\theta^z)]}\} \end{align}\tag{2.5}$

与CBOW模型一样利用梯度上升法对$\mathcal{L}$进行优化求最大值，将式(2.5)中花括号中的内容简记为$\mathcal{L}(w,u,z)$，然后将$\mathcal{L}(w,u,z)$分别对$v(w)$和$\theta^{z}$求偏导，具体求解过程省略，可参考文末链接参考1中的5.2节